CSES - Counting Tilings

Time Complexity: $\mathcal O(NM2^N)$.

Let $\texttt{dp}[i][j][mask]$ be the number of ways to tile the grid so that:

• All cells from cell $(0, 0)$ to cell $(i - 1, j)$ are covered.
• All cells from cell $(i, j + 1)$ to cell $(N, M)$ are empty.
• $mask$ represents whether each of the remaining $N$ cells are empty, with the $k$-th bit corresponding to the cell in column $k$.

For example, the following state would contribute toward $\texttt{dp}[4][2][10101_2]$:

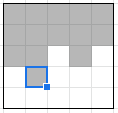
We now have two cases when calculating $\texttt{dp}[i][j][mask]$:

• The $j$-th bit of mask is 0, meaning that cell $(i, j)$ is covered.
  • Case 1: we used a vertical tile to cover it.
    • Cell $(i - 1, j)$ must have been empty before this, so there are $\texttt{dp}[i - 1][j][mask \oplus 2^j]$ ways to do this.
  • Case 2: we used a horizontal tile to cover it.
    • This is only possible if $j > 1$.
    • Cell $(i, j - 1)$ must have been empty before this, while cells $(i - 1, j - 1)$ and $(i - 1, j)$ must have been covered, so there are $\texttt{dp}[i][j - 2][mask]$ to do this.
• The $j$-th bit of the mask is 1, meaning that cell $(i, j)$ is empty.
  • Cell $(i - 1, j)$ must have been covered before this, so there are $\texttt{dp}[i - 1][j][mask \oplus 2^j]$ ways to do this.

Note that the indices we need to use may become negative and will thus require wrapping. To simplify calculations and bypass this, simply drop the first two dimensions of the DP array, as $\texttt{dp}[i][j]$ depends only on $\texttt{dp}[i][j - 1]$ and $\texttt{dp}[i][j - 2]$.

#include <bits/stdc++.h>
typedef long long ll;
using namespace std;

const ll MOD = 1e9 + 7;

ll dp[1 << 10][3];

int main() {
	cin.tie(0)->sync_with_stdio(0);